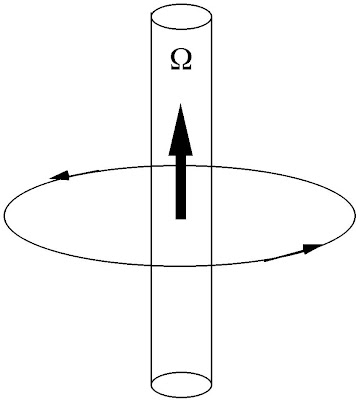
Vous le savez, les physiciens aiment approximer les choses. Nous utilisons donc l'approximation des tourbillons de Rankine, schématisé sur la figure de gauche. On suppose ainsi que le tourbillon est un cylindre parfait dont l'intensité des effets se mesure à l'aide de la circulation Ω. Le fluide entourant le "tourbillon" (ou vortex) est alors mis en rotation comme présenté sur la figure par le cercle et les flèches. On parle de vitesse angulaire Vθ, qui se calcule à l'aide de la formule : Vθ=Ω/2πr
 2. Écoulement fluide
2. Écoulement fluideEn se plaçant au dessus du tourbillon, on approxime le vortex par un point. En utilisant l'équation précédente, on peut alors calculer l'écoulement dans le plan.
À gauche, le champs de vitesse du fluide a été calculé pour un système de 3 points vortex, en utilisant Scilab. On voit que chaque point vortex a une vitesse qui est du à l'effet de ses voisins.
 3. États d'équilibre
3. États d'équilibrePour calculer la stabilité d'un système, on commence par définir son état d'équilibre. Dans notre cas, on dispose les points vortex de manière homogène sur un cercle.
Chaque point vortex a la même circulation Ω=1 et est disposé sur le cercle de rayon unité.
Chaque point vortex a la même circulation Ω=1 et est disposé sur le cercle de rayon unité.
4. Modèle numérique
On simule le comportement des points vortex en utilisation l'approximation de Rankine pour établir les équations de la dynamiques. L'algorithme de calcul est un Runge-Kutta à l'ordre 4. Les tests de convergence ont été faits sur des temps long avec 3 points vortex. En prenant pour grandeur de référence le rayon du cercle, la précision des positions des points vortex est de 10-6 après 107 pas de calculs. Sachant qu'il sont sur un cercle de rayon un, l'erreur est négligeable.
5. Système de 3 points vortex, linéairement stable-neutre
Sur la vidéo ci-dessous on voit un système de 3 points vortex. On perturbe le système en décalant légèrement un des points sur le cercle. On voit alors que les trajectoires ne sont plus sur le cercle parfait mais sont contenues dans une enveloppe. Si l'enveloppe grossit on parle d'instabilité. Si elle diminue pour redevenir un cercle on parle de stabilité au sens stricte. Cependant, l'enveloppe ne changeant pas, on parle alors d'une stabilité neutre car il reste des fréquences.
6. Non linéairement instable et bifurcation
 Un système de 7 points vortex faiblement perturbé est stable. Cependant en choisissant une perturbation suffisamment grande, on atteint un seuil critique de sorte que le point perturbé est piégé au centre du système. A gauche on voit la densité de probabilité de présence des vortex après 22 millions de pas de calcul, le point piégé apparait clairement au centre de la formation.
Un système de 7 points vortex faiblement perturbé est stable. Cependant en choisissant une perturbation suffisamment grande, on atteint un seuil critique de sorte que le point perturbé est piégé au centre du système. A gauche on voit la densité de probabilité de présence des vortex après 22 millions de pas de calcul, le point piégé apparait clairement au centre de la formation.
7. Système chaotique : 8 points vortex
 Avec 8 points vortex, le système est linéairement instable et il bascule dans le chaos. À gauche une image de la densité de probabilité de présence des vortex après 20 millions de pas de calcul. Les zones ne sont pas aussi contrastées que précédemment car les vortex alternent les un les autres au centre de la formation. De plus ils se désordonnent.
Avec 8 points vortex, le système est linéairement instable et il bascule dans le chaos. À gauche une image de la densité de probabilité de présence des vortex après 20 millions de pas de calcul. Les zones ne sont pas aussi contrastées que précédemment car les vortex alternent les un les autres au centre de la formation. De plus ils se désordonnent.
6. Non linéairement instable et bifurcation
 Un système de 7 points vortex faiblement perturbé est stable. Cependant en choisissant une perturbation suffisamment grande, on atteint un seuil critique de sorte que le point perturbé est piégé au centre du système. A gauche on voit la densité de probabilité de présence des vortex après 22 millions de pas de calcul, le point piégé apparait clairement au centre de la formation.
Un système de 7 points vortex faiblement perturbé est stable. Cependant en choisissant une perturbation suffisamment grande, on atteint un seuil critique de sorte que le point perturbé est piégé au centre du système. A gauche on voit la densité de probabilité de présence des vortex après 22 millions de pas de calcul, le point piégé apparait clairement au centre de la formation.7. Système chaotique : 8 points vortex
 Avec 8 points vortex, le système est linéairement instable et il bascule dans le chaos. À gauche une image de la densité de probabilité de présence des vortex après 20 millions de pas de calcul. Les zones ne sont pas aussi contrastées que précédemment car les vortex alternent les un les autres au centre de la formation. De plus ils se désordonnent.
Avec 8 points vortex, le système est linéairement instable et il bascule dans le chaos. À gauche une image de la densité de probabilité de présence des vortex après 20 millions de pas de calcul. Les zones ne sont pas aussi contrastées que précédemment car les vortex alternent les un les autres au centre de la formation. De plus ils se désordonnent.





0 comments:
Enregistrer un commentaire